How can investors measure the selection component of credit portfolios?
Investors who want to measure the selection performance of a credit portfolio are often confronted with the problem of having to make a simple but sufficiently precise measurement of this performance. Dr Harald Henke shows a way to achieve such a measurement.


Dr. Harald Henke
Head of Fixed Income Strategy
There are performance attribution methods that adjust the performance of a portfolio for all systematic effects and end up with a residual that is often interpreted as selection performance.
However, this approach has several drawbacks, including
- high complexity,
- lack of consideration of non-linear effects, which are then interpreted as selection effects, and
- the need for a large data base.
If an investor wants to know how much of the performance was due to higher carry and how much was due to the selection of better performing bonds on a risk-adjusted basis, we suggest that the average percentage change in a portfolio’s spread relative to the benchmark over a given period is a simple and intuitive measure of the selection component of a portfolio relative to a benchmark.
The idea can be illustrated with the following equation:
Equation (1)

Equation (1) was multiplied by -1 to flip the signs so that higher values of SCP represent higher selection performance. In this way, different portfolios with different risk and spread characteristics can also be compared.
Example: A portfolio with 100 basis points spread that experiences a spread widening of 10 basis points thus has the same selection performance as a portfolio with 150 basis points spread whose spreads widen by 15 basis points.
There is a very intuitive explanation for equation (1). If we expand the two quotients on the right-hand side of equation (1) with the average duration of the portfolio and the benchmark, Dt, respectively, we obtain the following equation:
Equation (2)
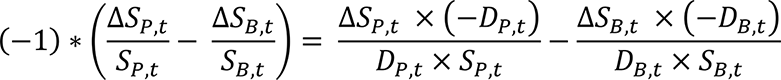
The right-hand side shows the quotient of the spread change return and the DTS for both the portfolio and the benchmark. Equation (2) and, through equivalence transformation, equation (1) thus measure the achieved spread change of the portfolio per unit of risk. Portfolios with a higher DTS also require a higher absolute spread change to show the same selection performance as a lower-risk portfolio.
SCP,t does not measure the total credit excess return. The positive carry return effect is explicitly not taken into account. The measure serves exclusively as an approximation to determine the selection performance of a portfolio, which takes different risk levels in the portfolio into account in a simple manner. Depending on the focus, the spread can be measured against a government bond or swap curve.
This measure is only an approximation of the selection performance of a portfolio. However, in a realistic scenario where the daily holdings of an asset manager’s portfolio are unknown and a performance attribution can therefore not be performed, the method presented allows a quick and meaningful analysis of the selection success of credit portfolios. Investors can use this method very easily.


